2.系外惑星の検出方法

　ここでは系外惑星の探索方法について述べます。
まず系外惑星の探索方法は大きく二つに分ける事が出来ます。

(1)直接検出

　これは一言でいうと、惑星の放つ光を捉える、つまり望遠鏡で直接惑星の像を捕らえる方法です。
ただし現在までこの方法で、存在が確認された太陽系外惑星は一つもありません。
　この方法には以下のような三つの問題点があるのです。

１．恒星と惑星の像の分解

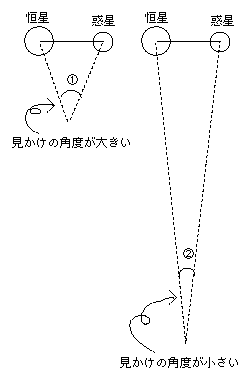
　図に示すように、二つの物体の張る見かけの角度（�@、�Aで示した角度）は観測位置から遠くなるほど小さくなるので、二つの物体を見分けるのは難しくなります。

太陽系外の天体は非常に遠いところにあるので、太陽系外の惑星がその主星と張る角度は極めて小さくなります。

　たとえばおおくま座47番星(14.08パーセク)は、現在惑星を二つ持つと考えられていますが、外側の惑星は、 主星(おおくま座47番星)から平均3.7天文単位(太陽系だと火星と木星の中間くらい) はなれたところにあります。
　これを地球から見た場合、主星と惑星がはる角度は0.2628秒角(3600秒角が１度)位になり、これは５００円玉(直径2.5cm)を 19.6ｋｍくらい離れたところから見るのと同じくらいの大きさです。

　そのため惑星の存在を捕らえるためには、分解能(*注1)の非常に高い望遠鏡が、必要になってきます。 望遠鏡の分解能は、光を集める鏡（またはレンズ）の口径が大きいほど高く、すなわち二つの物体のはる角度が 小さくても分離する事が出来るようになります。

　つまり太陽系外の惑星を見るためには、とても大きな望遠鏡を作る必要があるということになります。しかしそういった大望遠鏡をつくる技術は最近までありませんでした。
　最近、ケック望遠鏡やすばる望遠鏡をはじめとした、これまでは不可能とされてきた口径10メートル 程度の大望遠鏡が建設されるようになりましたが、これらの望遠鏡を以ってしても系外惑星の直接検出は 容易ではありません。

　望遠鏡の口径を大きくするのではなく干渉計というものを使って分解能を高めるという方法があります。
これは複数の望遠鏡（またはレンズや鏡）を配置し、それらで集めた光から元の物体像を再現するという 方法です。この時望遠鏡を100メートル離して配置すると口径100メートルの望遠鏡と同じ分解能を得る 事が出来ます。（ただし集光力は劣ります。）
　この方法を使えば一つの巨大望遠鏡を作るより簡単に高い分解能を得る事が出来るわけです。
(光学干渉計に関してはこちらのページ を参考にして下さい)

　口径10ｍの望遠鏡の理論分解能を計算 (注1に記載の式を使って) すると 波長500nm(0.5μm)の場合0.012秒角程度になります。
　上に書いた惑星と恒星がはる角度とくらべて、分解能だけ考えると現代の大望遠鏡なら系外惑星の 直接検出は容易におもえます。

　しかしKeckやすばるなどの大口径望遠鏡または、これら以上の分解能を持つ光学干渉計を作ったとしても 、以下に示すような問題があるのです。

２．星像のゆらぎ

　地球の大気は細かな塊に分かれ、それらが常にゆらいでいます。
これらの塊が一種のレンズのような働きをして星の像を、ぼかしてしまい期待通りの分解能が得られないのです。
　そのため口径の大きな望遠鏡を作っても、地球(地表)上では1秒角以下の分解能を実現するのは難しく理論通りの分解能が得らません。

　これをクリアする一つの方法として、ハッブル宇宙望遠鏡の様に地球大気の上に望遠鏡をあげる方法があります。
　たとえばハッブル宇宙望遠鏡(口径2.4m)の分解能は　0.05秒角程度です。
しかしこの方法は保守が大変であるとか、費用が非常に掛かるという点が大きな問題となります。

　問題をクリアするもう一つの方法は、何らかの方法によって大気の揺らぎによる星像のぼやけを キャンセルする事です。
　そのひとつとして補償光学と呼ばれる方法があります。その仕組みは観測する対象の近 くにある点光源と考えることの出来る天体を観測し(*注２)、その像の揺らぎから 大気の揺らぎを計算して、それに基ずいて望遠鏡の鏡を大気揺らぎの影響を打ち消すように変形すると いう方法です。

　またこれとは別の方法としてスペックル干渉法という方法があります。

　これらの技術にによって上記した二つの問題は、解決されつつあります。

３．恒星の惑星の放つ光の強度差

　ところが、惑星検出に十分な分解能を持った望遠鏡が、出来たとしてもまだ問題があります。
　惑星はその主星（恒星）に比べると、はるかに弱い光しか放っていません。そのような暗いものが上の１で述べたように、 明るい物の極めて近くに見えるのです。
そのため惑星の光は、主星の光に隠されて検出が難しいのです。

　例えとして、非常に光の強いサーチライトから10ｃｍ離れたところに、豆電球が光っていてそれを100メートル離れたところから見つける状況を想像して下さい。

　この問題を解決するために考えられるのが、ステラコロナグラフとナル干渉計など、何らかの方法で恒星からの光だけを 遮断してしまう方法です。
　これらの技術についてはこちらを見てください。

　ただし恒星の光をこれらの方法でさえぎったとしても、もともと惑星のだす光自体がとても弱いので、それを検出できる 大口径の望遠鏡や、微弱な光を捉える検出器の開発が必要になります。

(2)間接検出

　上に述べたような理由で、現在のところ惑星の直接検出はまだ難しく実際検出された太陽系外惑星は 、すべて間接的な方法で発見されています。
　間接的な方法としては、代表的なものとして次の三つが挙げられます。

(1)スペクトル線のドップラーシフトによる視線速度検出法
(2)Astrometory (恒星の固有運動(注３)の測定による方法)
(3)惑星が恒星を掩蔽する事を観測

　よく「惑星は太陽(恒星)の周りを回っている」とか、「月は地球の周りを回っている」という表現をし ます。しかし実際は惑星も月もその主星（太陽、地球）の中心より少し離れたところ（質量中心 いわゆる重心）を 回っていて恒星の方もこの質量中心のまわりを、まわっています。

もっと平たく言うと、恒星はその重力で惑星をひきつけている訳ですが、同じ様に惑星の方も恒星を引 き付けているので、そのため恒星は非常に僅かですが動くことになります。

　例えば太陽系に、太陽と木星しか存在しないとして太陽(の中心)の質量中心に対する軌道を計算すると下図の ように半径約 0.005 天文単位の楕円軌道を最大毎秒13メートル位の速度で動きます。

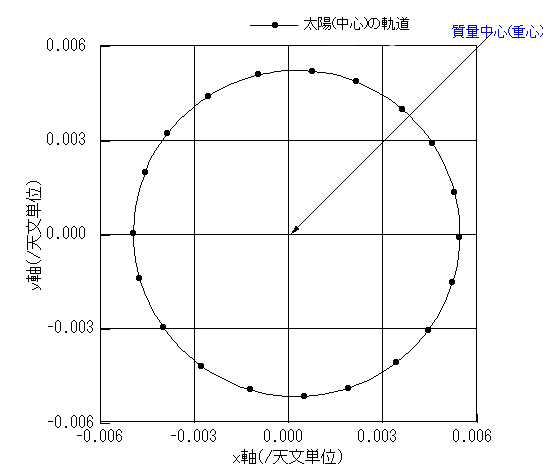
　この図のx=0、y=0 の点が質量中心です。横軸・縦軸の単位は天文単位になっていますが、太陽の半径を天文単位であらわすと0.0046天文単位くらいに なります。木星の軌道半径は約5天文単位で、それにくらべれば太陽の質量中心にたいする軌道半径は 1/1000 にすぎませんが、 それでも太陽半径とくらべると、かなり動いている事がわかります。
(なお実際の太陽は木星以外の惑星の影響もうけるので、もう少し複雑な動き方をします。)

１．スペクトル線のドップラーシフトによる視線速度検出法

　近ずいてくる物体から出てくる光は、その波長が青い(短い)方に、遠ざかる物体から出る光は波長が赤い(長い) 方に移動し物体の速度が大きいほど波長の変化量も大きくなります。これが光のドップラーシフトです。

　上で述べた様に恒星が動けば、周期的に地球に近ずいたり遠ざかったりするので恒星から出る光の波長も 周期的に変化します。
　下の図は、これを表したもので赤い丸が恒星、黒い丸が惑星をあらわします。惑星が直接観測できなくても 惑星の存在によって、恒星が軌道を描くのでこの恒星を観測していると（下の図で観測者は図の下側にいるとします）、 観測者に恒星が近づくとき恒星を出た光は波長が短くなり、遠ざかる時出た光は波長が長くなり、しかもこれは周期的に 変化します。

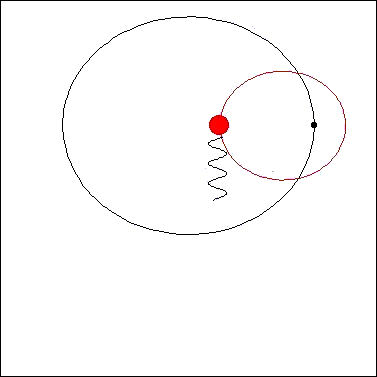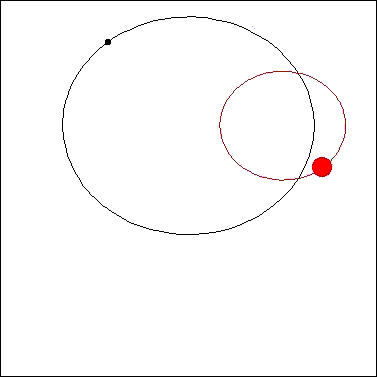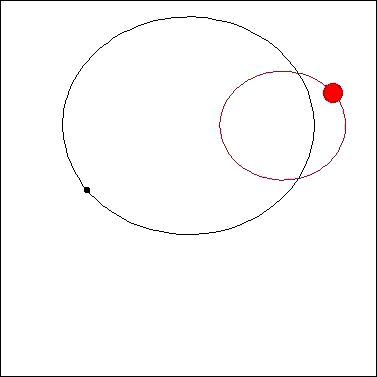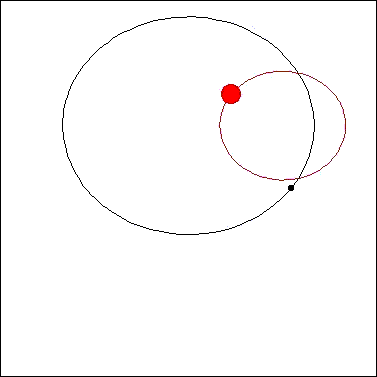
　したがって恒星からやってくる光の波長変化を調べる事で惑星や褐色わい星の存在を知る事が可能となります。
現在、発見されている系外惑星のほとんどは、この方法で発見されています。

実際観測された系外惑星のパラメータを入れて、この動きを計算したものを「惑星重力による恒星のふらつき」に載せたので 変化を確かめて下さい。

　なおこの方法には次のような欠点があります。
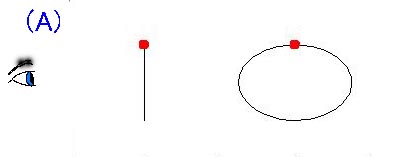
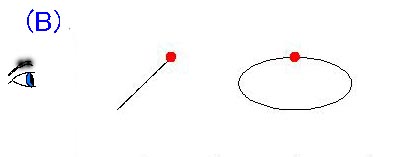
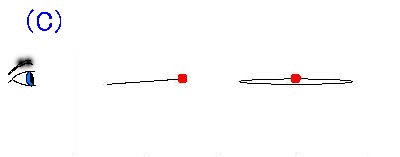
　下の図に示したように惑星(恒星)の公転面が、観測者(地球)にたいして垂直な場合(または垂直に近い場合)は、観測者に対して 運動しない(または運動が非常に小さくなる)ために、ドップラーシフトがおこらないので恒星の動きを検出する事が 出来ず、恒星が惑星を持っていてもその存在を知る事ができません。

　また、このためこの方法で推測できる惑星質量は、その質量の下限だけです。
(下にあげた掩蔽を利用した方法などと組み合わせて惑星の軌道面の視線方向に対する傾きを 知る事ができた場合にのみ真の質量がわかります)

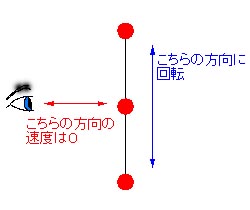
　なおこの図で赤い点は観測すべき恒星で目が観測者をあらわします。

２．恒星の固有運動の測定による方法( Astrometory )

　上で述べた視線速度検出法は恒星から発せられる光のドップラーシフトによって恒星の動きを捉えるものですが、 Astrometory というのは恒星の動きそのものを直接観測するものです。

　恒星は動かない星とされていますが（だから星座も毎年同じ形をしている訳ですが）、 実際は宇宙空間を運動しているので、非常に僅かですが移動しています。
　この恒星の運動のうち、地球から見た時のみかけの運動( 天球上に投影された運動 )を恒星の固有運動と呼びます。

　もし恒星の周りに惑星や不可視伴星が存在すると上記したように、それらに引っ張られて質量中心の周りを 公転し、この公転運動にくわえて宇宙空間を移動することになるので、地球から見ていると恒星が蛇行して動くように見えるはずです。

　たとえば、惑星がひとつしかない仮想的な太陽系を、惑星の軌道面に垂直な方向から観測した場合の恒星の動きを 下図に示してみました。
　下図の上側の図のように恒星が質量中心の周りを楕円軌道を描きながら図の右方向に等速運動する結果、 恒星は下側の図に示した軌道を描く事になります。

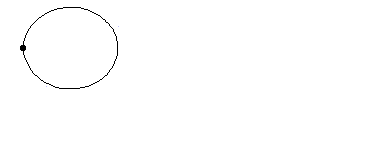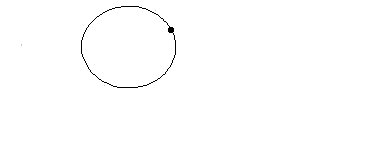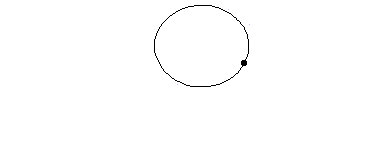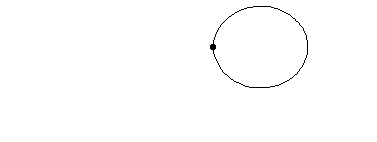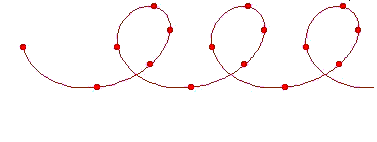　この動きを固有運動を観測する事で知り、そこから惑星の存在を推測するのがAstrometory による方法です。
　軌道は惑星(恒星)の公転周期や、恒星が空間を移動する速度で色々変化するので、それらから 惑星の軌道半径や質量を推察する事が可能になります。

　ただし実際の運動は上に述べたものに地球自身の公転運動が加わったりする上、観測されるふらつきの量は極めて小さいので 直接検出のところでのべたのと同じように観測には困難が伴います。

また視線速度法とは逆に、この方法は惑星(恒星)の公転面が、観測者(地球)にたいして垂直に近いほうが 観測しやすく(天球上に投影される軌道が大きくなるから)、逆に公転面が視線方向にあると恒星の動きの観測が難しくなるという特徴があって、視線速度法と 相補的な関係にあります。

　下に観測者に対して、軌道の傾斜面が垂直から水平になるにつれて、その天球面上へ投影される軌道が 小さくなっていくので観測が難しくなる事を示しました。
　実際はこの公転運動にくわえて恒星が天球面上を移動する運動が加わった動きが観察されます。

	軌道面の傾斜	天球面上の投影図

1960年代に系外惑星の「発見」(後にすべて誤りである事がわかった)が、報告された事がありましたが その検出方法は、このAstrometory によるものでした。

３．惑星による恒星の掩蔽(トランジット法)

　惑星が地球から見て恒星の前を通過すると、恒星の光が(ごく僅かですが)さえぎられその分、 光度が低下するはずです。この光度低下が恒星の周りを回る惑星によって引き起こされるものなら その変化が周期的におこるはずなので、これを観測しようという方法です。

　光度低下の周期から、惑星の公転周期が求められ、恒星の質量がわかっている場合、周期から 惑星軌道の長半径を求めることができます。
　また光度の減少率から、恒星の半径がわかっている場合、惑星の半径を求めることが出来ます。
　この方法だけでは、惑星の質量を求めるのは困難ですが、光度曲線の解析から惑星軌道の視線方向に 対する傾斜角を求めることが出来るので、視線速度法と組み合わせることで、 惑星の質量を求めることが可能となります。

　このようにして惑星の半径と質量が求められるので、惑星の(平均)密度を計算することが可能になり、 惑星が木星のようなガス惑星なのか、地球のように岩石や金属からなる惑星なのかを知ることが出来るようになります。

　ただし、この方法が可能になるには惑星の公転面が、観測者の視線方向とほぼ同じ方向に向いていなければ 観測することができません。
　そういった都合のいい配置の惑星系は確率的に低いと考えられています。
　またいつ惑星の恒星面通過が、起こるかわかりませんからこの方法で成果を挙げるにはたくさんの対象(恒星)を 長時間にわたって観測する必要があるので、地上からの観測には困難がありました。

　Kepler などの探査機では、これらの欠点が克服されめざましい成果が上がっています。

　以前この方法は、近接連星を発見するのに使われてきました。
この方法によってHD209458という星系で、惑星によると考えられる恒星の光度低下が観測されていました。

　この方法を使って天文アマチュアによって系外惑星の観測を行なおうとする動きがあります。詳しくは「系外惑星を探れ!」 (星ナビ.com内のページ)を見てください。