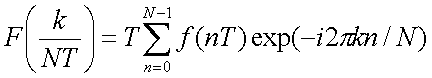 | ...(1) |
一次元関数 f(x) を離散化したうえで数値的にフーリエ変換する方法とそのプログラムを以下で
紹介します。
なおここでの計算方法は「光とフーリエ変換」の「5.高速フーリエ変換」を参考にしています。
(ただしこのページに載せたプログラムは独自に作成したものです)
2007年1月24日 説明を一部追加するとともに「6.プログラム使用上の注意」を追加しました
まず f(x) を間隔Tに離散化して x= n*T (nは整数)の値のみを考えるようにし、さらに n を0からN-1 までの
N個の点に制限します。
この離散化関数を、フーリエ変換したものをF(ν) とします。(引数 νは周波数になります)
この段階で F(ν)は周波数に対して連続関数となっていますが、次にこれを離散化します。
元の関数 f(x) を間隔TのN個の点に離散化したことにより、フーリエ変換した式は間隔 1/(N*T) で離散化することに
なります(詳しい事は上の参考文献や、高速フーリエ変換に関する本を参照してください。)。
離散化した結果の式を書くと以下の様になります。なおこの式で k は0からN-1の値をとる整数で、引数の k/( N*T) は
離散化した周波数のk-1番目(k =0 が1番目だから)の値を表します。
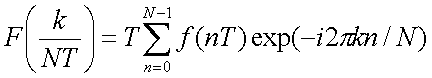 | ...(1) |
注意 :以下の式では(1)式のΣの前に掛けてある間隔T が省略されています。また例として 載せているプログラムでもこのTが掛けてないので、実際に使用するときは間隔Tを掛けるように修正してください。
(1)式で F( k/NT) をF(k)に、f( nT )をf(n)に、exp(-i2π/N) を W と書き換えて下の(2)式のように
簡単に書くことにします。
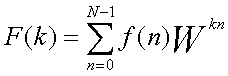 | ...(2) |
まず離散点の数Nを、N = r1*r2 と二つの数の積に分解します。
つぎに以下に示すようにk を二つの数k0、k1で、n も同じように二つの数n0、n1を
使って書き直します。
|
k =k1r1 + k0 n =n1r2 + n0 |
k1 =0,1,...r2-1 k0 =0,1,...r1-1 n1 =0,1,...r1-1 n0 =0,1,...r2-1 |
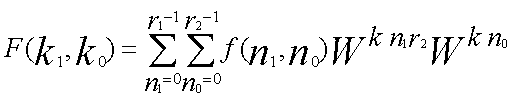 | ...(3) |
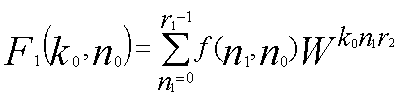 | ...(4-2) |
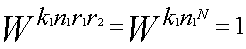 を利用して
を利用して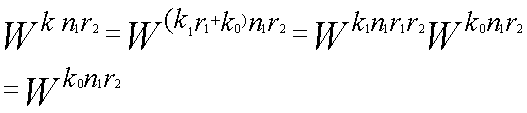 を(4-2)に使った。
を(4-2)に使った。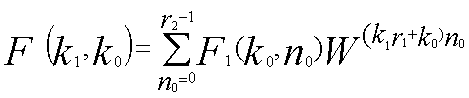 | ...(4-1) |
ここではN=2m の場合のより具体的な手順について記します。
①r1=2、r2= N /2 の場合
|
k =2k1 + k0 n =(N/2)n1 + n0 |
k1 =0,1,...(N/2)-1 k0 =0,1 n1 =0,1 n0 =0,1,...(N/2)-1 |
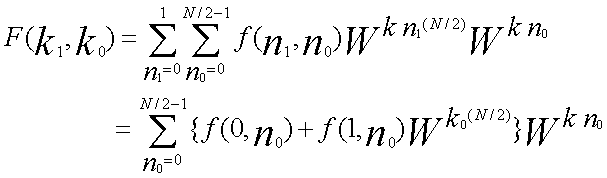 | ...(5) |
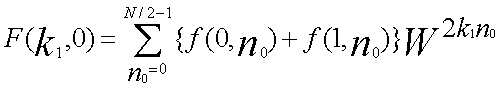 | ...(5-1) |
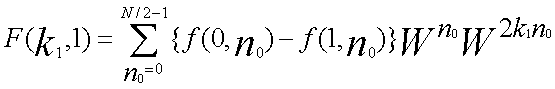 | ...(5-2) |
|
k1 =2k'1 + k'0 n0 =(N1/2)n'1 + n'0 |
k'1 =0,1,...(N1/2)-1 k'0 =0,1 n'1 =0,1 n'0 =0,1,...(N1/2)-1 |
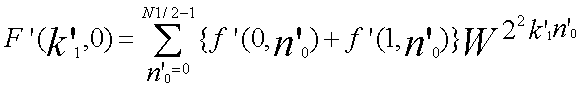 | ...(6-1) |
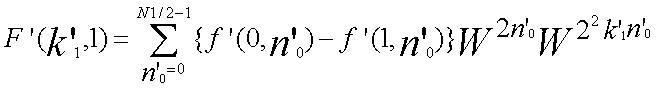 | ...(6-2) |
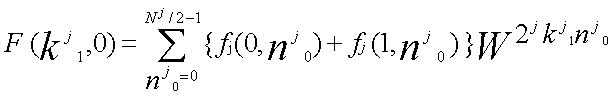 | ...(7-1) |
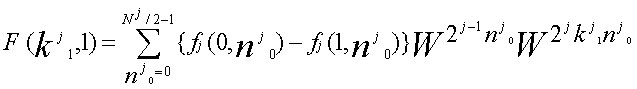 | ...(7-2) |
|
F(0) F(1) F(2) F(3) F(4) F(5) F(6) F(7) |
F(0) F(2) F(4) F(6) |
F(0) 0=(000)--->(000) F(4) 1=(001)--->(100) |
| F(2) 2=(010)--->(010) F(6) 3=(011)--->(110) |
||
| F(1) F(3) F(5) F(7) |
F(1) 4=(100)--->(001) F(5) 5=(101)--->(101) |
|
| F(3) 6=(110)--->(011) F(7) 7=(111)--->(111) |
プログラムは C++ で書いてあります。ソースファイルの拡張子は cpp にしておいて下さい。
以下に各部分について簡単な説明を入れておきます。
関数 DecimFrq_FFTCall が計算の本体で第一引数に計算したい関数を離散化した値を収めた配列を与えます。
この配列に計算したフーリエ変換値をいれて送り返すので、元の関数の値を保持しておきたいときには注意してください。
なおこのフーリエ変換値には式(1)に掛けてある間隔 T が掛けてないので注意してください。
この引数は complex
第二引数は第一引数の配列要素数を与えてください。
DecimFrq_FFT は繰り返し計算をおこなう部分です。
CalcRev_BinaryExp は計算結果の順番を入れ替えている部分です。
|
/*
高速フーリエ変換 周波数間引き法プログラム 関数宣言ファイル 関数の分割数が2^N のもの */ #ifndef ___fastfrt #define ___fastfrt #include <complex> using namespace std; //introduces namespace std /*
//高速フーリエ変換計算部分
//二進表記で逆の順にした数値を作成
//与えた数値が2^N の形をしているか調べる
|
|
#include "fftdef.h"
#include <cmath> /* func_array ==>計算終了時はフーリエ変換したものが入っている
/*
}
/*
return num_revby ;
/*
} |