「視線速度計算」で用いた軌道計算に関する式

1.Ver1.3までの軌道計算法の概要

Ver.1.3までは系外惑星系の軌道計算を行うのに、ケプラーの方程式

u - e*sin( u ) = n*(t-t0)
ただしuは離心近点角、eは離心率、ｎは平均運動、t0は近日点を通過する時刻、tは時刻を表す。
　(これらの用語の意味については天体力学に関する書籍を見てください。)
を解いて求めますが、その際離心近点角や位置座標などを離心率でべき級数展開しました。

したがって離心率が0に近いところでは低い次数でよい結果を与えますが離心率が大きくなるにつれより高い項まで取る必要が生じます。

Ver1.3では6次まで展開して計算していましたが、離心率が0.5を越えると結果は怪しくなってきます。

2.Ver1.4での軌道計算法の概要

　Ver1.4では、ケプラーの方程式を解くのではなく、二体問題の運動方程式を直接(数値的・4次のRungeKutta法を使用)解き、 それを用いてドップラーシフトや視線方向速度の計算をおこないます。

　まず二つの質点(これが主星と伴星、または恒星とその周りを回る惑星をあらわします)が重力相互作用 (万有引力)だけを、及ぼしている場合の運動方程式を重心系で考えます。

　ここでは、軌道面をxy平面にとるものとしｚ軸方向の運動はないものとします。
　この場合、質点1の(重心系における)運動方程式は、以下の様に表されます。

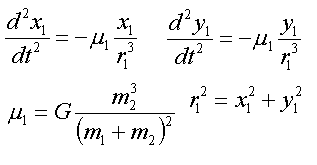
重心系の運動方程式

　ここでm1、m2はそれぞれ質点1、2の質量、x1、y1は質点1のx、y座標の値、Gは万有引力定数を表します。

　また質点2の位置(x2,y2)と速度は、重心系では重心が原点にあることから質点1の位置、速度を使って
質点2の速度と座標 の様にして求める事が出来ます。

　次に上の運動方程式を次の様に一階微分のみの式に変形します。

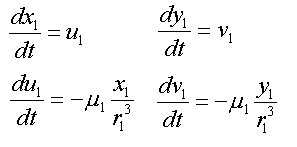
一階微分使用運動方程式

　ただしパラメータにMKSA単位系やCGS単位系の値を入れて数値計算しようとすると精度が悪くなるので、 μ1(と、質点１の近日点距離)を1にするような単位系を取って上の運動方程式式を変形します。

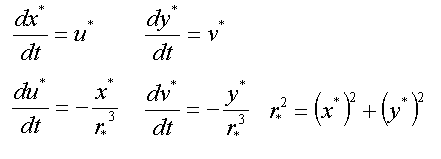
単位変換運動方程式

　後はこの式をRunge-Kutta法や、修正Euler法等の方法によって時間パラメータtを離散化して 解けばよいのですが、Ver1.4ではさらに上の式をより精度よく(離散化が荒くても精度の高い解が得られる) 解けるように、以下の様に変形します(「数値計算の常識」伊里正夫・藤野和建著　共立出版株式会社　第12章を参照)
　新しい独立変数sを導入し時間tもsの関数になります。よって離散化するのはtではなくsになります。

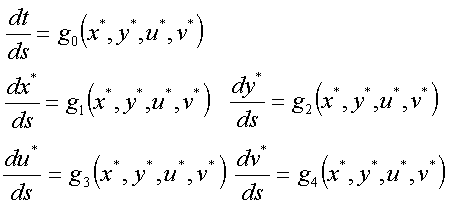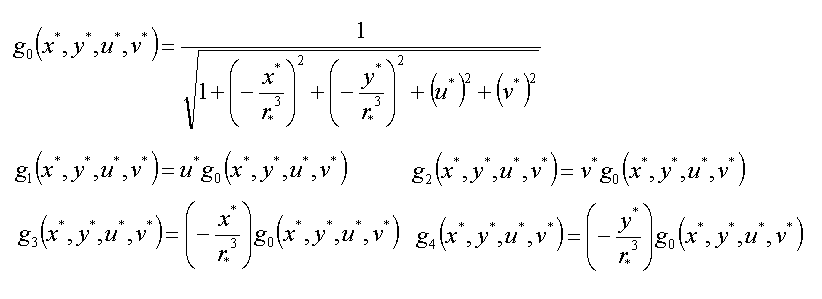変形運動方程式 変形運動方程式

　Ver1.4では上の方程式を４次のRunge-Kutta法で解いて(重心系の)座標と速度の時間変化を求め、その値を 元にして視線方向速度やドップラーシフトの計算をおこないます。

[系外惑星関連ソフトに戻る]