2016年10月16日
[物理学]
[物理学]
バイクペダルにかかる力の方程式
\[F_{\rm p}=F_{\rm w} \times \frac{R_{\rm w}}{R_{\rm p}} \times \frac{R_{ f \rm -g}}{R_{r \rm -g}}\]
自分はロードバイクを持っているのだが，初めてロードバイクに乗った時に迷ったのは変速の仕方であった．ロードバイクを買うまでに自分が乗ったことがある自転車は，すべてギアが後輪だけについていた．そして，ギアの半径が小さな方にチェーンを動かせば，ペダルが重たくなる分，ひと漕ぎで進む距離が増えるというのが普通であった．
ところが，ロードバイクに乗ってみると，ギアが後輪だけではなく，ペダルの部分（正しくはクランクという）にもついている．そして，後輪のギアとは逆に，ギアの半径が大きくなるほうにチェーンを動かせばペダルが重たくなるのである．はじめてこのことに気づいたときは不思議だったが，すぐには理由がわからず，そのうち気にせず乗るようになっていった．
しかし，ある時ふと考え直してみると，このことはエネルギー保存則から説明できることに気付いた．それで，腰を据えて立式してみると，上の方程式にたどり着いたのである．
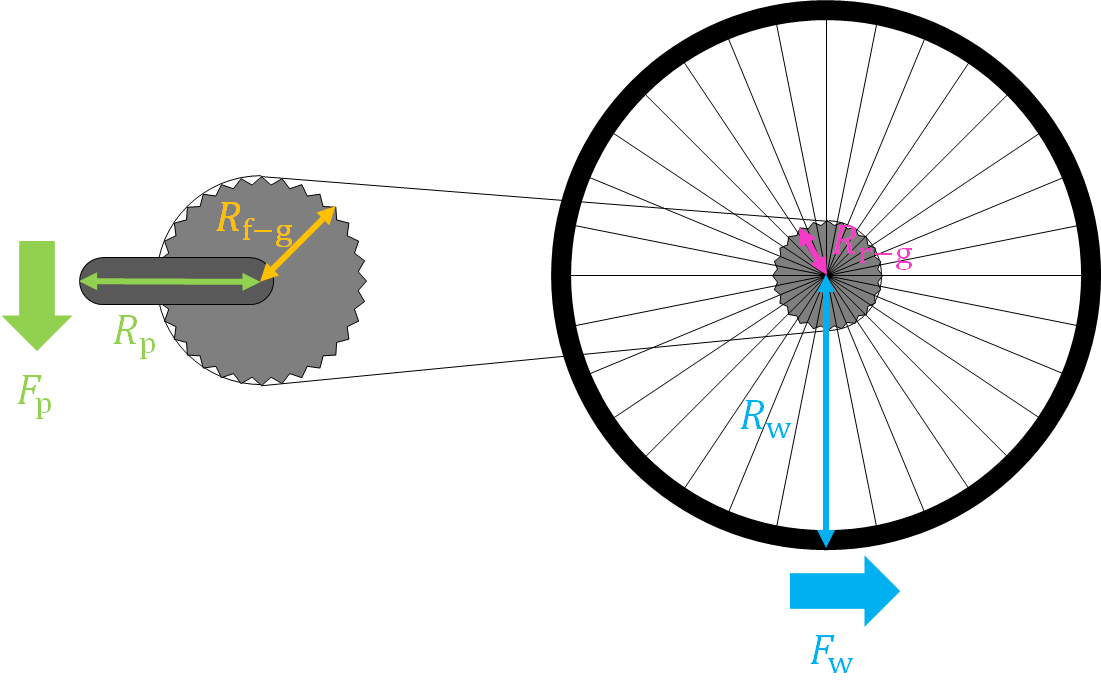それでは，タイトルの方程式の導出過程について説明しよう．まず，ロードバイクを漕いでいるときに，各部分にかかる力について定義しておく．上の図を見てほしい．ロードバイクを漕いでいるとき，漕ぐ足の力はまずペダルに伝わる．この力をFpとする．Fpはチェーンを通じて後輪のギアに伝えられ，最終的に後輪を動かす力Fwとなる．次に，ロードバイクの各部分の長さを定義する．ペダルの回転軸の中心から足で踏んでいるところまでの長さをRpとする．ペダルと連結しているフロントギアの半径をRf-gとし，後輪と連結しているリアギアの半径をRr-g，後輪の半径はRwとする．
ここまで出来たら，いよいよエネルギー保存則の登場である．ここでは，ペダルがする仕事は全て後輪が回転するエネルギーに変換されると仮定する．ペダルを1回転させた時にペダルがする仕事をW1とすると，
\[ W_1 = F_{\rm p} \times 2\pi R_{\rm p}\]
となる．次に，ペダルが1回転したときに，後輪が動く距離について考える．ペダルが1回転するとフロントギアも1回転する．フロントギアとチェーンで連結しているリアギアは当然フロントギアと同じ距離を動く．そのため，リアギアの回転数はフロントギアが1回転した時に移動する距離を，リアギアが1回転した時に移動する距離で割ったものとなり，リアギアの回転数をnとすると，
\[ n= \frac{2\pi R_{f \rm -g}}{2\pi R_{r \rm -g}} = \frac{R_{f \rm -g}}{R_{r \rm -g}} \]
となる．リアギアの回転数と，後輪の回転数は等しいので，ペダルが1回転した時に後輪がする仕事をW2とすると，
\begin{align} W_2 &= F_{\rm w} \times 2\pi R_{\rm w} \times n \\ &= F_{\rm w} \times 2\pi R_{\rm w} \times \frac{R_{f \rm -g}}{R_{r \rm -g}} \end{align}
となる．エネルギー保存則から，W1=W2であるから，
\begin{align} F_{\rm p} \times 2\pi R_{\rm p} &= F_{\rm w} \times 2\pi R_{\rm w} \times \frac{R_{f \rm -g}}{R_{r \rm -g}} \\ \therefore F_{\rm p} &= F_{\rm w} \times \frac{R_{\rm w}}{R_{\rm p}} \times \frac{R_{ f \rm -g}}{R_{r \rm -g}} \end{align}
こうして，タイトルの方程式が導出された．
この方程式中の一番右側の分数は，ペダルにかかる力がフロントギアの半径Rf-gに比例し，リアギアの半径Rr-gに反比例することを表している．これが，自分がロードバイクに初めて乗った時に感じた不思議の理由であるが，結局これは，ペダルが1回転したときの後輪の回転数が多いほど，ペダルにかかる力は大きいということを表している．また，この方程式の真ん中の分数は，ペダルにかかる力が後輪の半径Rwに比例し，ペダルの回転軸の中心から足で踏んでいるところまでの長さRpに反比例することを意味している．つまり，折り畳み自転車のように車輪の小さい自転車はひと漕ぎが軽く，一方，三輪車のようにペダルが短いとひと漕ぎが重いということである．
エネルギー保存則から，ロードバイクの変速機構の不思議に答えることができた．それにしても，ロードバイクを発明した人はこういうメカニズムをよく思いついたなあと思う．前後のギアを用いた変速機構があるから，平坦な道は重いギアを回して快走できるし，急な上り坂は軽いギアでじりじり登れて，ロードバイクの幅が広がるのだと思う．
ところが，ロードバイクに乗ってみると，ギアが後輪だけではなく，ペダルの部分（正しくはクランクという）にもついている．そして，後輪のギアとは逆に，ギアの半径が大きくなるほうにチェーンを動かせばペダルが重たくなるのである．はじめてこのことに気づいたときは不思議だったが，すぐには理由がわからず，そのうち気にせず乗るようになっていった．
しかし，ある時ふと考え直してみると，このことはエネルギー保存則から説明できることに気付いた．それで，腰を据えて立式してみると，上の方程式にたどり着いたのである．
ここまで出来たら，いよいよエネルギー保存則の登場である．ここでは，ペダルがする仕事は全て後輪が回転するエネルギーに変換されると仮定する．ペダルを1回転させた時にペダルがする仕事をW1とすると，
\[ W_1 = F_{\rm p} \times 2\pi R_{\rm p}\]
となる．次に，ペダルが1回転したときに，後輪が動く距離について考える．ペダルが1回転するとフロントギアも1回転する．フロントギアとチェーンで連結しているリアギアは当然フロントギアと同じ距離を動く．そのため，リアギアの回転数はフロントギアが1回転した時に移動する距離を，リアギアが1回転した時に移動する距離で割ったものとなり，リアギアの回転数をnとすると，
\[ n= \frac{2\pi R_{f \rm -g}}{2\pi R_{r \rm -g}} = \frac{R_{f \rm -g}}{R_{r \rm -g}} \]
となる．リアギアの回転数と，後輪の回転数は等しいので，ペダルが1回転した時に後輪がする仕事をW2とすると，
\begin{align} W_2 &= F_{\rm w} \times 2\pi R_{\rm w} \times n \\ &= F_{\rm w} \times 2\pi R_{\rm w} \times \frac{R_{f \rm -g}}{R_{r \rm -g}} \end{align}
となる．エネルギー保存則から，W1=W2であるから，
\begin{align} F_{\rm p} \times 2\pi R_{\rm p} &= F_{\rm w} \times 2\pi R_{\rm w} \times \frac{R_{f \rm -g}}{R_{r \rm -g}} \\ \therefore F_{\rm p} &= F_{\rm w} \times \frac{R_{\rm w}}{R_{\rm p}} \times \frac{R_{ f \rm -g}}{R_{r \rm -g}} \end{align}
こうして，タイトルの方程式が導出された．
この方程式中の一番右側の分数は，ペダルにかかる力がフロントギアの半径Rf-gに比例し，リアギアの半径Rr-gに反比例することを表している．これが，自分がロードバイクに初めて乗った時に感じた不思議の理由であるが，結局これは，ペダルが1回転したときの後輪の回転数が多いほど，ペダルにかかる力は大きいということを表している．また，この方程式の真ん中の分数は，ペダルにかかる力が後輪の半径Rwに比例し，ペダルの回転軸の中心から足で踏んでいるところまでの長さRpに反比例することを意味している．つまり，折り畳み自転車のように車輪の小さい自転車はひと漕ぎが軽く，一方，三輪車のようにペダルが短いとひと漕ぎが重いということである．
エネルギー保存則から，ロードバイクの変速機構の不思議に答えることができた．それにしても，ロードバイクを発明した人はこういうメカニズムをよく思いついたなあと思う．前後のギアを用いた変速機構があるから，平坦な道は重いギアを回して快走できるし，急な上り坂は軽いギアでじりじり登れて，ロードバイクの幅が広がるのだと思う．