2016年11月3日
[数学]
[数学]
十分条件と必要条件
\[\underset{十分条件}{p} \Longrightarrow \underset{必要条件}{q} \]
2つの条件p，qについて命題「p⇒q」が真であるとき，pはqであるための十分条件であり，qはpであるための必要条件である，という．このことを，条件pを満たすものの集合をP，条件qを満たすものの集合をQとすると，以下の図のようになる．
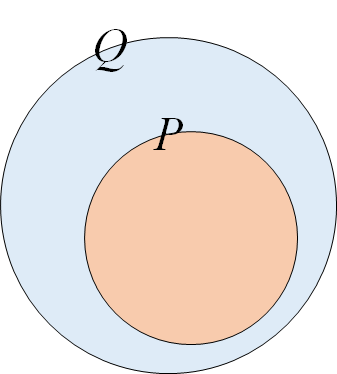つまり，十分条件というのは，pであれば必ずqであると言っていいということである．一方，必要条件というのは，qはpであるためには必要だけど，qだからといってpであるとは限りませんよということである．
具体例を挙げると，「東京に住んでいる」ということは「日本に住んでいる」ということの十分条件である．なぜなら，東京は日本に必ず含まれるからである．一方，「日本に住んでいる」ということは「東京に住んでいる」ということの必要条件である．なぜなら，東京に住んでいるなら日本に住んでいるということは間違いないが，日本には東京以外にも神奈川とか埼玉とか住むところがあるからである．
世間には必要条件と十分条件の関係性が整理されず，誤解されていることが多いように思う．自分が気になっているのは，「安全」と「安心」というキーワードである．一見すると，「安全」と「安心」は同じことのように見える．多くの人も，この2つのキーワードはセットで使っていると思われる．しかし，よくよく考えてみると，この2つのキーワードの間には，必要条件も十分条件も成り立っていない．
例えば，「安全」ならば「安心」である，という命題は成り立つだろうか．仮にこの命題が真であるならば，「風評被害」という言葉がマスコミで取り上げられることはないだろう．客観的な事実に基づく「安全」と，個人の主観に基づく「安心」との間には，大きなズレがあると言わざるを得ない．また，「安心」ならば「安全」である，という命題は成り立つだろうか．原発を建設した当時は「安心」であることを謳っていただろうが，震災による被害を見ると「安全」であったとはいえない．
このような論理学の考え方は，物事を落ち着いて分析する際には役に立つと思う．
具体例を挙げると，「東京に住んでいる」ということは「日本に住んでいる」ということの十分条件である．なぜなら，東京は日本に必ず含まれるからである．一方，「日本に住んでいる」ということは「東京に住んでいる」ということの必要条件である．なぜなら，東京に住んでいるなら日本に住んでいるということは間違いないが，日本には東京以外にも神奈川とか埼玉とか住むところがあるからである．
世間には必要条件と十分条件の関係性が整理されず，誤解されていることが多いように思う．自分が気になっているのは，「安全」と「安心」というキーワードである．一見すると，「安全」と「安心」は同じことのように見える．多くの人も，この2つのキーワードはセットで使っていると思われる．しかし，よくよく考えてみると，この2つのキーワードの間には，必要条件も十分条件も成り立っていない．
例えば，「安全」ならば「安心」である，という命題は成り立つだろうか．仮にこの命題が真であるならば，「風評被害」という言葉がマスコミで取り上げられることはないだろう．客観的な事実に基づく「安全」と，個人の主観に基づく「安心」との間には，大きなズレがあると言わざるを得ない．また，「安心」ならば「安全」である，という命題は成り立つだろうか．原発を建設した当時は「安心」であることを謳っていただろうが，震災による被害を見ると「安全」であったとはいえない．
このような論理学の考え方は，物事を落ち着いて分析する際には役に立つと思う．