2016年10月1日
[数学]
[数学]
交代調和級数
\[\rm 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots=ln2\]
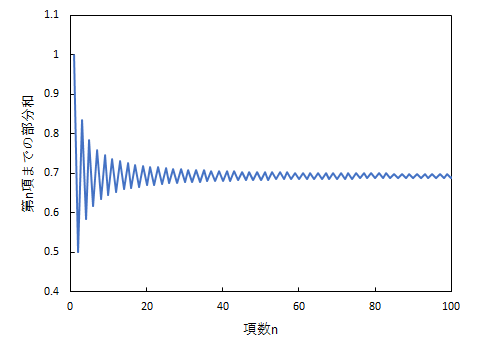
ln(1+x)のマクローリン展開にx=1を代入すると，上の交代調和級数が得られ，それは2の自然対数に収束する．下の図は，級数の収束の様子を表していて，横軸に項数，縦軸にその項数までの部分和をとってある．部分和がln2≒0.693に近づいて行く様子がよくわかる．
上の図はExcelを用いて計算したのだが，それにしてもコンピュータというのは便利な物で，100個の分数を足し引きするという計算も一瞬でできてしまい，グラフもほぼ自動で描けてしまう．コンピュータが無かった時代には，こういった計算や，グラフの描画もすべて手作業だったと思うと，当時の人たちの根気の良さに感心してしまう．
話を無限級数に戻すと，こういった無限級数が初等関数で表せる例は他にもいくつかある．自分は数学に精通しているわけでもないし詳しいところはわからないが，一見全く違う者同士が実は同じことを表しているということは，数の世界には見えないつながりがたくさんあるということだと思う．
話を無限級数に戻すと，こういった無限級数が初等関数で表せる例は他にもいくつかある．自分は数学に精通しているわけでもないし詳しいところはわからないが，一見全く違う者同士が実は同じことを表しているということは，数の世界には見えないつながりがたくさんあるということだと思う．